ANASEN: Difference between revisions
| Line 45: | Line 45: | ||
== Tracking for the twisted wire configuration == | == Tracking for the twisted wire configuration == | ||
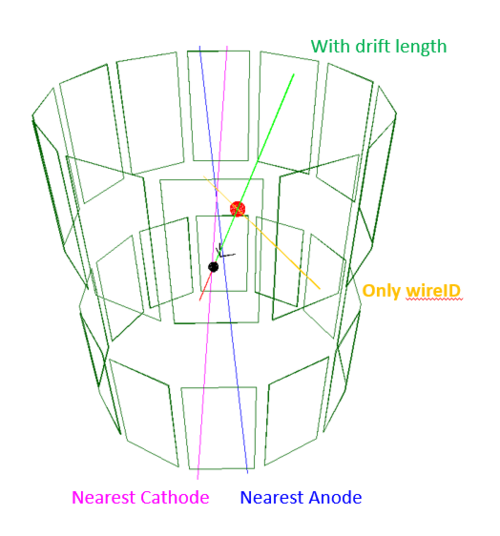
A beam trace consists of 5 parameters: 3 from a point <math> (x_0, y_0, z_0)</math> and 2 from the trace angle <math> (\ | A beam trace consists of 5 parameters: 3 from a point <math> (x_0, y_0, z_0)</math> and 2 from the trace angle <math> (\theta, \phi)</math>. Thus, to reconstruct the beam trace, we need at least 5 pieces of information. | ||
Suppose we know the position on the SuperX3, thus, we have 3 pieces of information <math> \vec{p_0} = (x_0, y_0, z_0)</math>. And We have 2 wires ID. Each wire and the <math>\vec{p_0} </math> will form a plan, the intersection line of the 2 plans will give us the first approximation of the beam trace. | Suppose we know the position on the SuperX3, thus, we have 3 pieces of information <math> \vec{p_0} = (x_0, y_0, z_0)</math>. And We have 2 wires ID. Each wire and the <math>\vec{p_0} </math> will form a plan, the intersection line of the 2 plans will give us the first approximation of the beam trace. | ||
Each wire is constructed from 2 points, let them be <math> \vec{a_i} </math> and <math> \vec{b_i} </math>, where <math> i </math> is the wire ID. The plan formed by the points <math> \vec{p_0}, \vec{a_i}, \vec{b_i} </math> has normal <math> \vec{n_i} = (\vec{p_0} - \vec{a_i}) \times (\vec{p_0} - \vec{b_i}) </math>. The vector for the line intersects between the 2 plans constructed by wire ID <math> i, j</math> and point </math> \vec{p_0}</math> is <math> \vec{N_{ij}} = \vec{n_i} \times \vec{n_j} </math>. Thus, the beam trace has an equation of <math> \vec{r} = \vec{p_0} + s \vec{N_{ij}} </math>, where <math> s </math> is the coordinate on the line. | Each wire is constructed from 2 points, let them be <math> \vec{a_i} </math> and <math> \vec{b_i} </math>, where <math> i </math> is the wire ID. The plan formed by the points <math> \vec{p_0}, \vec{a_i}, \vec{b_i} </math> has normal <math> \vec{n_i} = (\vec{p_0} - \vec{a_i}) \times (\vec{p_0} - \vec{b_i}) </math>. The vector for the line intersects between the 2 plans constructed by wire ID <math> i, j</math> and point </math> \vec{p_0}</math> is <math> \vec{N_{ij}} = \vec{n_i} \times \vec{n_j} | ||
: (\theta, \\phi)</math>. Thus, the beam trace has an equation of <math> \vec{r} = \vec{p_0} + s \vec{N_{ij}} </math>, where <math> s </math> is the coordinate on the line. | |||
Since the beam is not hit directly on the wires, but a distance <math> d_i </math> from the wire. This will rotate the plane on <math> \vec{p_0} </math> along the direction <math> \vec{a_i} - \vec{b_i} </math> by <math> \pm \arctan{d/l} </math>, where <math> l </math> is the perpendicular distance of the point <math> \vec{p_0} </math> and the line. This creates 2 additional planes with normal vectors that are rotated along the line by angle <math> \pm \arctan{d/l} </math>. The 4 additional planes form the uncertainty boundaries of the beam. In other words, the normal vector of the plane has uncertainty <math> \vec{n_i} \pm \vec{d_i} </math> that translates to the beam direction vector <math> \vec{N_{ij}} : (\theta \pm \delta\theta, \phi \pm \delta\phi) </math>. | |||
Revision as of 02:04, 14 January 2024
Array for Nuclear Astrophysics and Structure with Exotic Nuclei (ANASEN) is an active target detector. FSU, LSU, and TAM are joined in the development of the project.
First Generation
NIM paper : https://doi.org/10.1016/j.nima.2017.07.030 PRC paper : https://doi.org/10.1103/PhysRevC.105.055806
Second Generation
The main difference from the 1st generation is the Twisted Anode and Cathode wires.
Basics Geometry
There are 5 Layers on the radial position of the ANASEN.
| Structure | Radius [mm] |
|---|---|
| ionizing wires | 23 |
| Graurd wires | 33 |
| Anode wires | 38 |
| Cathode wires | 43 |
| SuperX3 Silicon | 88 |
Twisted Anode and Cathodes
Readout
SuperX3 Silicon Detector Array
There are 24 Super-X3 double-sided Silicon detectors on the wall of the ANASEN. They are placed 88 mm away from the beam axis. Each of them has 75 mm X 40 mm sensitive area. Thus, the super-X3 covers a forward and backward angle of 40 deg.
Readout
Tracking for the twisted wire configuration
A beam trace consists of 5 parameters: 3 from a point and 2 from the trace angle . Thus, to reconstruct the beam trace, we need at least 5 pieces of information.
Suppose we know the position on the SuperX3, thus, we have 3 pieces of information . And We have 2 wires ID. Each wire and the will form a plan, the intersection line of the 2 plans will give us the first approximation of the beam trace.
Each wire is constructed from 2 points, let them be and , where is the wire ID. The plan formed by the points has normal . The vector for the line intersects between the 2 plans constructed by wire ID and point </math> \vec{p_0}</math> is Failed to parse (syntax error): {\displaystyle \vec{N_{ij}} = \vec{n_i} \times \vec{n_j} : (\theta, \\phi)} . Thus, the beam trace has an equation of , where Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s } is the coordinate on the line.
Since the beam is not hit directly on the wires, but a distance Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_i } from the wire. This will rotate the plane on Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{p_0} } along the direction Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{a_i} - \vec{b_i} } by Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pm \arctan{d/l} } , where Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l } is the perpendicular distance of the point Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{p_0} } and the line. This creates 2 additional planes with normal vectors that are rotated along the line by angle Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pm \arctan{d/l} } . The 4 additional planes form the uncertainty boundaries of the beam. In other words, the normal vector of the plane has uncertainty Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{n_i} \pm \vec{d_i} } that translates to the beam direction vector Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{N_{ij}} : (\theta \pm \delta\theta, \phi \pm \delta\phi) } .