ANASEN

Array for Nuclear Astrophysics and Structure with Exotic Nuclei (ANASEN) is an active target detector. FSU, LSU, and TAM are joined in the development of the project.

First Generation

NIM paper : https://doi.org/10.1016/j.nima.2017.07.030 PRC paper : https://doi.org/10.1103/PhysRevC.105.055806

Second Generation

Section of ANASEN with twisted wire configuration

A simulation, showed the Anode wires, the Cathode wites, the SuperX3 Silicon Detector, and QQQ Silicon Detector. The simulation shows Anode-9 and Cathode-15 are hit.

The main difference from the 1st generation is the Twisted Anode and Cathode wires.

Basics Geometry

There are 5 Layers on the radial position of the ANASEN.

Structure	Radius [mm]
ionizing wires	23
Graurd wires	33
Anode wires	38
Cathode wires	43
SuperX3 Silicon	88

SuperX3 Silicon Detector Array

A drawing of SuperX3 silicon detector

There are 24 Super-X3 double-sided Silicon detectors on the wall of the ANASEN. They are placed 88 mm away from the beam axis. Each of them has 75 mm X 40 mm sensitive area. Thus, the super-X3 covers a forward and backward angle of 40 deg.

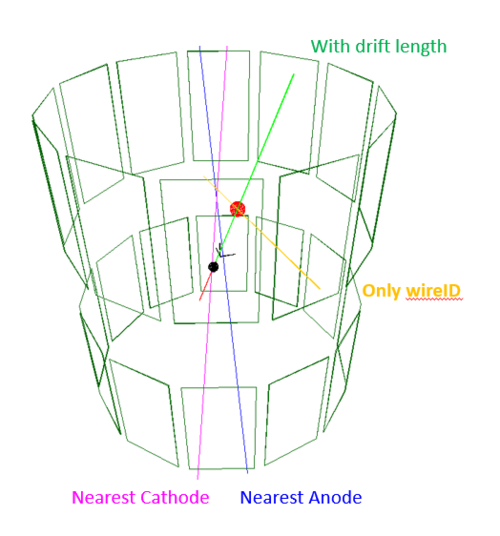
Tracking for the twisted wire configuration

A beam trace consists of 5 parameters: 3 from a point $(x_{0},y_{0},z_{0})$ and 2 from the trace angle $(\theta ,\phi )$. Thus, to reconstruct the beam trace, we need at least 5 pieces of information.

Suppose we know the position on the SuperX3, thus, we have 3 pieces of information ${\vec {p_{0}}}=(x_{0},y_{0},z_{0})$. And We have 2 wires ID. Each wire and the ${\vec {p_{0}}}$ will form a plan, the intersection line of the 2 plans will give us the first approximation of the beam trace.

Each wire is constructed from 2 points, let them be ${\vec {a_{i}}}$ and ${\vec {b_{i}}}$, where $i$ is the wire ID. The plan formed by the points ${\vec {p_{0}}},{\vec {a_{i}}},{\vec {b_{i}}}$ has normal ${\vec {n_{i}}}=({\vec {p_{0}}}-{\vec {a_{i}}})\times ({\vec {p_{0}}}-{\vec {b_{i}}})$. The vector for the line intersects between the 2 plans constructed by wire ID $i,j$ and point </math> \vec{p_0}</math> is ${\vec {N_{ij}}}={\vec {n_{i}}}\times {\vec {n_{j}}}:(\theta ,\phi )$. Thus, the beam trace has an equation of ${\vec {r}}={\vec {p_{0}}}+s{\vec {N_{ij}}}$, where $s$ is the coordinate on the line.

Since the beam is not hit directly on the wires, but a distance $d_{i}$ from the wire. This will rotate the plane on ${\vec {p_{0}}}$ along the direction ${\vec {a_{i}}}-{\vec {b_{i}}}$ by $\pm \arctan {d/l}$, where $l$ is the perpendicular distance of the point ${\vec {p_{0}}}$ and the line. This creates 2 additional planes with normal vectors that are rotated along the line by angle $\pm \arctan {d/l}$. The 4 additional planes form the uncertainty boundaries of the beam. In other words, the normal vector of the plane has uncertainty ${\vec {n_{i}}}\pm {\vec {d_{i}}}$ that translates to the beam direction vector ${\vec {N_{ij}}}:(\theta \pm \delta \theta ,\phi \pm \delta \phi )$.